Back in July, we built a software module to “guarantee” that a quadcopter never leaves a rectangular box. We spent months proving this guarantee as a mathematical theorem. We were pretty proud of ourselves, until we actually bothered to run our code. As it turns out, when it comes to cyber-physical systems, there’s more to it then just proving theorems.

The problem

The purpose of the software module, which we call a monitor, is to allow the pilot or existing control software to move the quadcopter freely within a rectangular region but prevent it from ever leaving that rectangular region.

Quadcopter inside boundary	Quadcopter approaching boundary

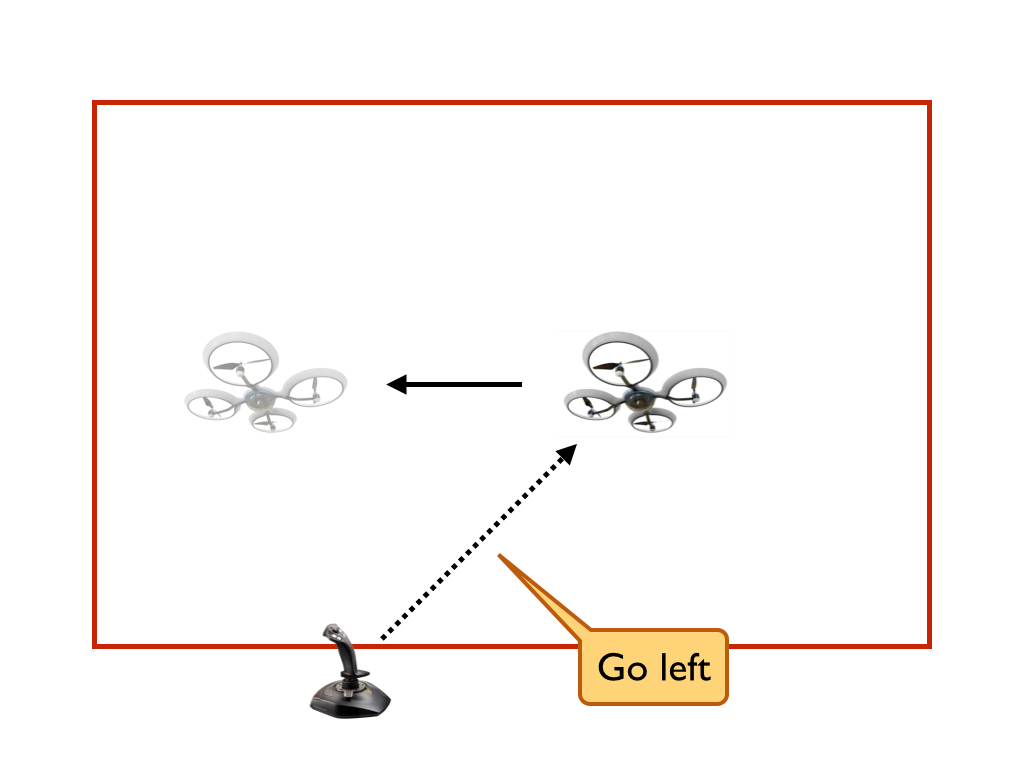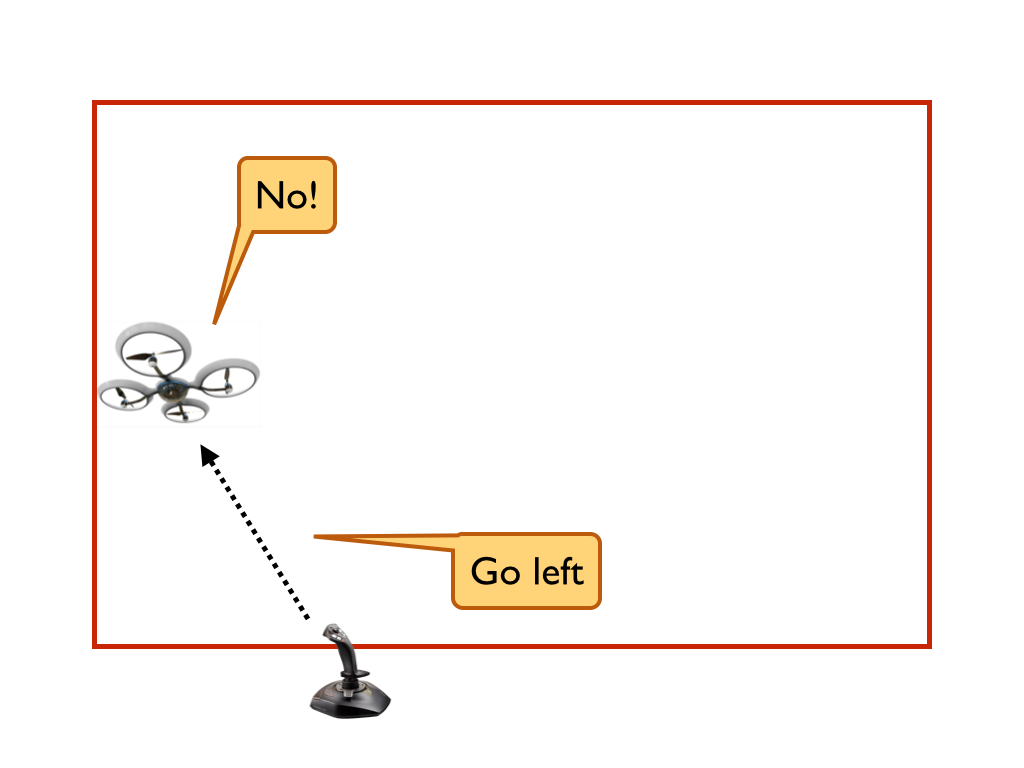We proved that our monitor guarantees that the quadcopter will never leave the safe rectangular box, assuming a simple model of the quadcopter dynamics. This is a key point. In particular, our model doesn’t include a number of forces like wind. So as it turns out, when you actually fly a quadcopter with our monitor, it does occasionally leave the rectangular safe region. Minor violations are ok; in fact, they are inevitable in this domain since a model of the physical dynamics can never include all the details. But what happens when the quadcopter leaves the rectangular safe region? As the following figure depicts, the quadcopter gets stuck:

A prior post discusses why the quadcopter gets stuck. To summarize, while running our rectangular bounding monitor, when the quadcopter was pushed outside any of the boundaries by wind or other unmodeled forces, the logic of the monitor prevented the quadcopter from moving back inside the boundaries, regardless of what the pilot did. In this post, I’m going to describe potential solutions to this issue.

Potential solutions

This issue is not a violation of any property we verified. Within our model of the dynamics of the quadcopter, the monitor prevents the quadcopter from ever leaving the rectangular boundaries, so there is no need to prove anything about what happens when the quadcopter is outside. However, when working with cyber-physical systems, there is always a gap between model and reality. In order to build a practical verified monitor, we need to verify something about what happens when the quadcopter is outside the boundaries enforced by the monitor. What exactly should we verify?

Informally, we want the quadcopter to behave reasonably with respect the the safe region defined by the monitor’s boundaries. For example, we want the quadcopter to stay close to the safe region if it starts close and to eventually move back inside the safe region if it starts outside. Moreover, we want whatever property we verify to reduce to our original safety property when the quadcopter starts within the safe region (i.e. the quadcopter stays within the safe region if it starts within the safe region¹).

These informal notions of reasonable behavior are very similar to several core notions in control theory called Lyapunov stability. Roughly speaking, Lyapunov stability characterizes the behavor of a system of differential equations around an equilibrium (a point $x_e$ such that if the system is initially at $x_e$, then it remains at $x_e$ for all time). There are three common notions of stability in the theory of Lyapunov:

1. A system is Lyapunov stable if it can remain within any distance $\epsilon$ of the equilibrium as long as it starts within some distance $\delta$ of the origin. In other words, a system will remain arbitrarily close to the equilbirium as long as it starts sufficiently close.
2. A system is asymptotically stable if it is Lyapunov stable and approaches the equilibrium as time goes to infinity. In other words, the system remains close to the equilibrium and eventually converges to it.
3. A system is exponentially stable if it is asymptotically stable and if the distance to the equilibrium over time is bounded by an exponential function. In other words, the system remains close to the equilbirium and converges exponentially quickly to it.

These three definitions of stability seem to capture the kind of reasonable behavior I described earlier, except that our system (a quadcopter equiped with our rectangular bounding monitor) does not have an equibrium point. In other words, there is no single point such that if the quadcopter reaches that point, it should remain there for all time. However, we do have a region such that if the system reaches that region, it should remain there for all time. This region is the safe region. We can easily adapt the three notions of stability to our setting by replacing “distance to the equilibrium” with “distance to the safe region”.

Now we have three definitions of stability that apply to our setting. Which one do we actually use? The first definition, Lyapunov stable, does not require that the system ever re-enter the safe region if it leaves the safe region, so it permits the system to remain stuck on the boundary. The second definition, asymptotic stability, does require the system to converge to the safe region, but there is no bound on how long this must take. For all practical purposes, this could still allow the system to remain stuck on the boundary. Thus, it seems that the final definition, exponential stability, is the appropriate one. It requires not only that the system converge to the safe region but that it do so quickly.

We have not yet verified or tested the appropriateness of stability for capturing reasonable behavior of the quadcopter outside of the safe region. In fact, stability is not the only potential solution to our problem. Here are a couple other potential solutions that we are considering:

1. We could treat the problem as an optimization problem in which the monitor seeks to minimize some notion of “badness”. One possible definition of badness is the distance from the safe region. There is a tremendous amount of work on optimial control theory that we could draw from.

2. The quadcopter only leaves the safe region if there are unmodeled forces such as wind. What happens when there is a constant unmodeled force like a constant wind? Even an exponentially stable system may not converge to the safe region in the presence of a constant wind. Thus, we may want to verify that the system quickly converges to the safe region in the presence of such an unmodeled force. Again, there are ideas from control theory that we can draw on, such as the use of the I term in a PID controller.

We haven’t yet experimentally evaluated any of these ideas, but as always, this is very important. As soon as we do so, we will certainly write another blog post on the results.