In an earlier post, I mentioned that the first test of our rectangular bounding monitor had a few interesting problems, and I described one of them. In this post, I’ll describe another interesting problem that occurred during the test, and the cause that we later discovered.

The problem

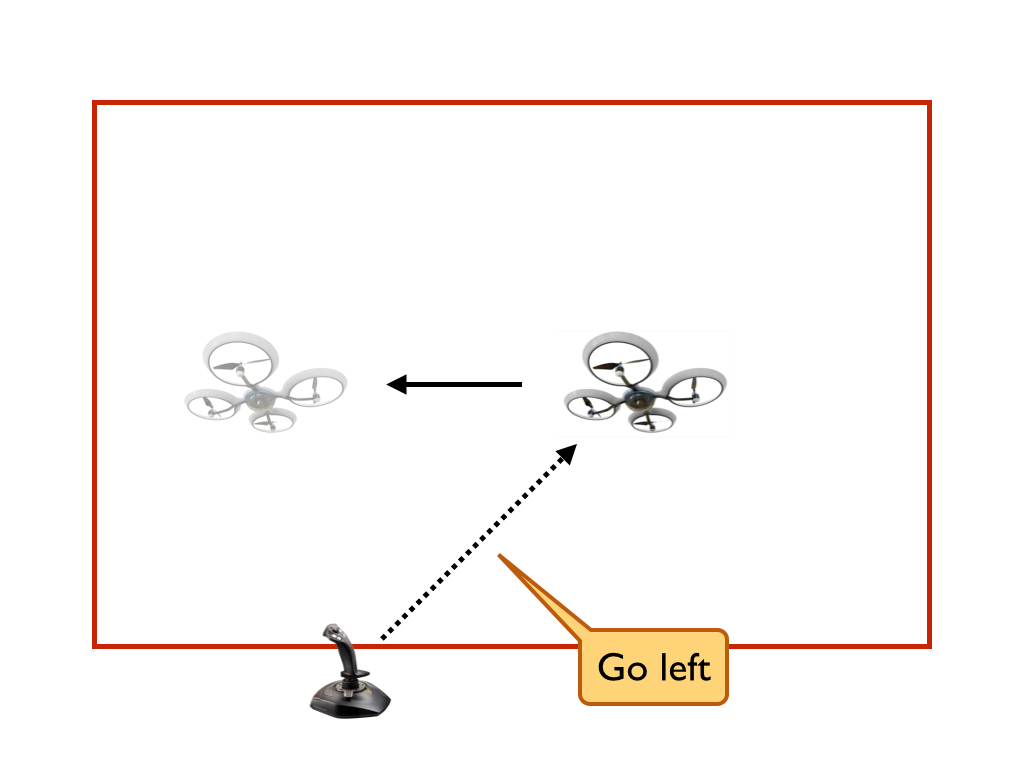
The purpose of the monitor is to allow the pilot or existing control software to move the quadcopter freely within a rectangular region but prevent it from ever leaving that rectangular region.

Quadcopter inside boundary	Quadcopter approaching boundary

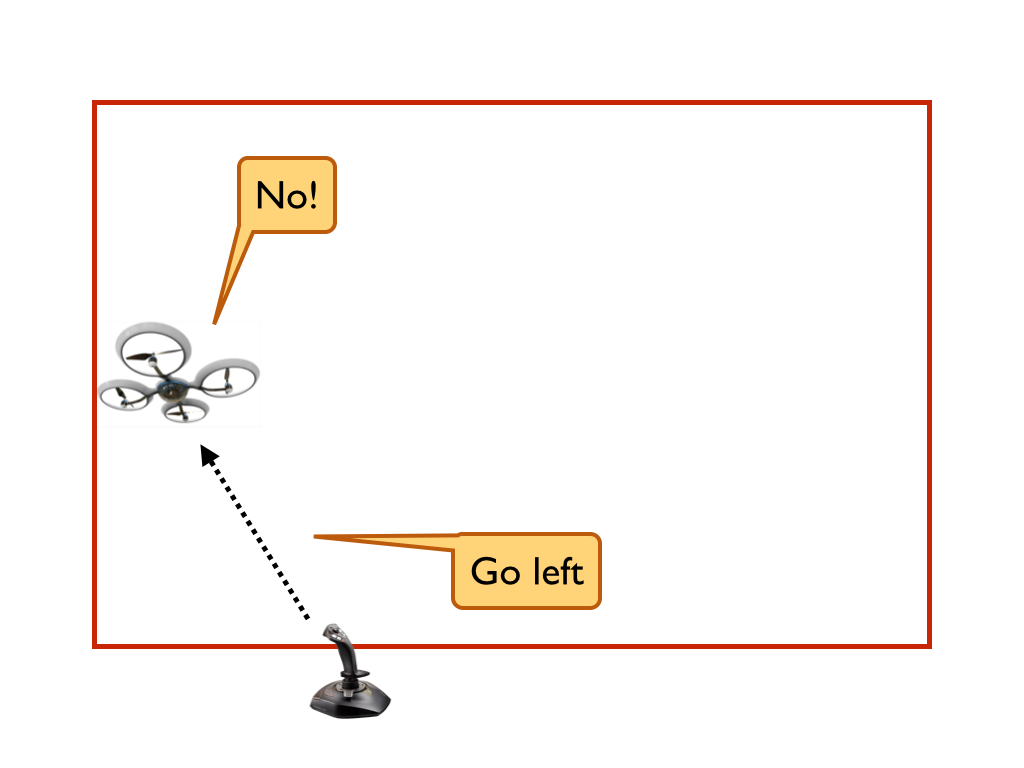When the quadcopter was on the border of the bounding box, it sometimes appeared to get stuck. That is, when Sorin attempted to move the quadcopter towards the middle of the bounding box, the monitor ignored his comments, even though they seemed to be perfectly safe.

This didn’t always occur when the quadcopter was on the boundary; it only occurred sometimes.

The cause

In the earlier post, I gave the following pseudo-code for the monitor:

AX = A*sin(Theta)
AZ = A*cos(Theta)

if (Safe(AX,...) && Safe(AZ,...)) {
  issue A and Theta
} else if (Safe(AZ,...) && ...) {
   issue polar(AZ, defaultX)
} else if (Safe(AX,...) && ...) {
   issue polar(defaultZ, AX)
} else {
   issue polar(defaultZ, defaultX)
}

The monitor first converts the pilot’s desired roll angle (Theta) and acceleration (A) to rectangular coordinates, and then checks them for safety, taking different actions depending on which safety checks pass (see the earlier post for more details).

At first glance, it doesn’t seem like this would cause the quadcopter to get stuck at the boundaries. As long as the quadcopter remains within bounds, the monitor should always allow the pilot to steer the vehicle back towards the center of the bounding box.

Unfortunately, the quadcopter does not always stay within bounds; it occasionally leaves the box by a small amount, generally less than 1 meter. While this might seem to indicate that our formal verification result is useless, this sort of violation is actually inevitable in cyber-physical systems. The theorem that we prove in Coq is only with respect to a model of the physical world, and no model can account for everything (e.g. wind). To take an extreme example, if a tornado flies into the bounding box, the quadcopter might not stay inside.

Thus, no matter how detailed our model is, we should account for the possibility that the quadcopter leaves the bounding box. Let’s go back to the code to take a look at what happens when the quadcopter is outside one of the boundaries. As it turns out, the safety checks will reject any desired acceleration from the pilot, even if it will bring the quadcopter back inside the boundary. Thus, the monitor will take the last branch, issuing the default accelerations for both dimensions:

issue polar(defaultZ, defaultX)

The default accelerations issued by the monitor aren’t actually fixed. Instead, the monitor uses the following logic (independently in each dimension):

1. If the vehicle is moving towards the middle of the bounding box, issue acceleration of 0.
2. If the vehicle is moving away from the middle of the bounding box, issue acceleration of amin < 0.

There is a more detailed explanation of amin in this post, but for our purposes here, it is any value less than 0.

Now suppose that the vehicle is stationary (zero velocity) outside the upper bound in the X dimension. The monitor will issue an acceleration of amin in the X dimension, causing the quadcopter to start moving back towards the middle of the box in the X dimension. However, the next time the monitor runs (every 0.01 seconds), it will issue an acceleration of 0.

In a world with no unmodeled forces, the vehicle will eventually move back inside the bounding box, at the velocity induced by accelerating at amin for 0.01 seconds. However, we do not live in such a world. In reality, the quadcopter will be stuck until the wind pushes it back inside the boundaries, or the default action of the monitor inches it back inside.

Prior to observing the quadcopter getting stuck in a flight test, we didn’t consider verifying anything about what happens outside the bounding box. However, this test has shown us that we should. The reality is that unmodeled forces can always push the system outside its bounds, so the monitor should behave reasonably in those situations. In a future post, I’ll talk about the precise property we should verify in order to ensure this reasonable behavior.