> {-# LANGUAGE TypeSynonymInstances, FlexibleContexts, NoMonomorphismRestriction, OverlappingInstances, FlexibleInstances #-}> import Control.Monad.Error
> import Control.Monad.State
> import Control.Monad.Writer
> import Debug.Trace
> import Control.ApplicativeLets recall the simple language of divisions.
> data Expr = Val Int
> | Div Expr Expr
> deriving (Show)Today, we will see how monads can be used to write (and compose) evaluators for such languages.
Remember the vanilla unsafe evaluator
> eval :: Expr -> Int
> eval (Val n) = n
> eval (Div x y) = eval x `div` eval yHere are two terms that we will use as running examples.
> ok = Div (Div (Val 1972) (Val 2)) (Val 23)
> err = Div (Val 2) (Div (Val 1) (Div (Val 2) (Val 3)))The first evaluates properly and returns a valid answer, and the second fails with a divide-by-zero exception.
ghci> eval ok
42
ghci> eval err
*** Exception: divide by zeroWe didn’t like this eval because it can just blow up with a divide by zero error without telling us how it happened. Worse, the error is a radioactive value that, spread unchecked through the entire computation.
We used the Maybe type to capture the failure case: a Nothing result meant that an error happened somewhere, while a Just n result meant that evaluation succeeded yielding n. Morever, we saw how the Maybe monad could be used to avoid ugly case-split-staircase-hell.
> evalMaybe :: Expr -> Maybe Int
> evalMaybe (Val n) = return n
> evalMaybe (Div x y) = do n <- evalMaybe x
> m <- evalMaybe y
> if m == 0
> then Nothing
> else return (n `div` m)which behaves thus
ghci> evalMaybe ok
Just 42
ghci> evalMaybe err
NothingThe trouble with the above is that it doesn’t let us know where the divide by zero occurred. It would be nice to have an exception mechanism where, when the error occurred, we could just saw throw x for some value x which would, like an exception go rocketing back to the top and tell us what the problem was.
If you think for a moment, you’ll realize this is but a small tweak on the Maybe type; all we need is to jazz up the Nothing constructor so that it carries the exception value.
> data Exc a = Exn String
> | Result a
> deriving (Show)Here the Exn is like Nothing but it carries a string denoting what the exception was. We can make the above a Monad much like the Maybe monad.
> instance Monad Exc where
> (Exn s ) >>= _ = Exn s
> (Result x) >>= f = f x
> return = Result> instance Functor Exc where
> -- fmap :: (a -> b) -> Exc a -> Exc b
> fmap f (Exn s) = Exn s
> fmap f (Result x) = Result (f x)> instance Applicative Exc where
> pure = Result
> -- (<*>) :: Exc (a -> b) -> Exc a -> Exc b
> Exn x <*> _ = Exn x
> _ <*> Exn x = Exn x
> Result f <*> Result x = Result (f x)Throwing Exceptions
Let’s write a function to throw an exception
throw = Exnand now, we can use our newly minted monad to write a better exception throwing evaluator
> class Monad m => MonadRandom m where
> getRandom :: m Int> foo :: (MonadRandom m) => m a -> m (a, Int)
> foo act = do
> x <- act
> i <- getRandom
> return (x, i)> evalExc :: Expr -> Exc Int
> evalExc (Val n) = return n
> evalExc (Div x y) = do n <- evalExc x
> m <- evalExc y
> if m == 0
> then throw $ errorS y m
> else return $ n `div` mwhere the sidekick errorS generates the error string.
> errorS y m = "Error dividing by " ++ show y ++ " = " ++ show mNote that this is essentially like the first evaluator; instead of bailing with Nothing we return some (hopefully) helpful message, but the monad takes care of ensuring that the exception is shot back up.
ghci> evalExc ok
Result 42
ghci> evalExc err
Exn "Error dividing by Div (Val 2) (Val 3) = 0"Catching Exceptions
Its all well and good to throw an exception, but it would be nice if we could gracefully catch them as well. For example, wouldn’t it be nice if we could write a function like this:
> evalExcc :: Expr -> Exc (Maybe Int)
> evalExcc e = tryCatch (Just <$> evalExc e) $ \err ->
> return ({- trace ("oops, caught an exn" ++ err) -} Nothing)Thus, in evalExcc we have just caught the exception to return a Maybe value in the case that something went wrong. Not the most sophisticated form of error handling, but you get the picture.
What should the type of tryCatch be?
Exc a -> (a -> Exc b) -> Exc bExc a -> (String -> Exc a) -> Exc a
> tryCatch :: Exc a -> (String -> Exc a) -> Exc aAnd next, lets write it!
> tryCatch (Exn err) f = f err
> tryCatch r@(Result _) _ = rAnd now, we can run it of course…
ghci> evalExcc ok
Result (Just 42)
ghci> evalExcc err
Caught Error: Error dividing by Div (Val 2) (Val 3) = 0
Result NothingNext, lets stop being so paranoid about errors and instead try to do some profiling. Lets imagine that the div operator is very expensive, and that we would like to count the number of divisions that are performed while evaluating a particular expression.
As you might imagine, our old friend the state-transformer monad is likely to be of service here!
> type StateST = Int
> data ST a = S (StateST -> (a, StateST))
>
> instance Functor ST where
> instance Applicative ST where
>
> instance Monad ST where
> return x = S $ \s -> (x, s)
> (S st) >>= f = S $ \s -> let (x, s') = st s
> S st' = f x
> in st' s'Next, lets write the useful runStateST which executes the monad from an initial state, getST and putST which allow us to access and modify the state, respectively.
getST = S (\s -> (s, s))
putST = \s' -> S (\_ -> ((), s'))Armed with the above, we can write a function
> tickST = do n <- getST
> putST (n+1)Now, we can write a profiling evaluator
> evalST :: Expr -> ST Int
> evalST (Val n) = return n
> evalST (Div x y) = do n <- evalST x
> m <- evalST y
> tickST
> return (n `div` m)and by judiciously making the above an instance of Show
> runST :: ST a -> (a, Int)
> runST (S st) = st 0
>
> instance Show a => Show (ST a) where
> show m = "value: " ++ show x ++ ", count: " ++ show s
> where
> (x, s) = runST mwe can get observe our profiling evaluator at work
ghci> evalST ok
value: 42, count: 2But, alas, to get the profiling we threw out the nifty error handling that we had put in earlier
ghci> evalST err
value: *** Exception: divide by zero(Hmm. Why does it print value this time around?)
So it looks like Monads can do many thigs, but only one thing at a time – you can either use a monad to do the error management plumbing OR to do the state manipulation plumbing, but not at the same time. Is it too much ask for both? I guess we could write a mega-state-and-exception monad that supports the operations of both, but that doesn’t sound like any fun at all! Worse, if later we decide to add yet another feature, then we would have to make up yet another mega-monad.

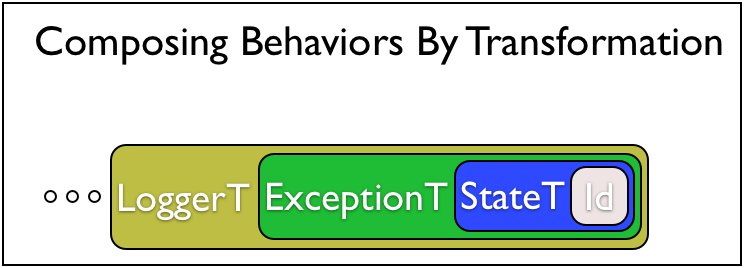
We shall take a different approach, where we will keep wrapping or decorating monads with extra features, so that we can take a simple monad, and then add the Exception monad’s features to it, and then add the State monad’s features and so on.
The key to doing this is to not define exception handling, state passing etc as monads, but as functions from monads to monads. This will require a little more work up-front (most of which is done already in well-designed libraries) but after that we can add new features in a modular manner. For example, to get a mega state- and exception- monad, we will start with a dummy Identity monad, apply it to the StateT monad transformer (which yields state-passing monad) and pass the result to the ExcT monad transformer which yields the desired mega monad. Incidentally, the above should remind some of you of the Decorator Design Pattern and others of Python’s Decorators.
Concretely, we will develop mega-monads in four steps:
Step 1: Description First we will define typeclasses that describe the enhanced monads, i.e. by describing their extra operations,
Step 2: Use Second we will see how to write functions that use the mega monads, simply by using a combination of their features – here the functions’ type signatures will list all the constraints on the corresponding monad,
Next, we need to create monads with the special features. We will do this by starting with a basic powerless monad, and then
Step 3: Add Features thereby adding extra operations to the simpler monad to make it more powerful, and
Step 4: Preserver Features Will make sure that the addition of features allows us to hold onto the older features, so that at the end, we get a mega monad that is just the accumulation of all the added features.
Next, lets look at each step in turn.
The first step to being able to compose monads is to define typeclasses that describe monads armed with the special features. For example, the notion of an exception monad is captured by the typeclass
> class Monad m => MonadExc m where
> throw :: String -> m awhich corresponds to monads that are also equipped with an appropriate throw function (you can add a catch function too, if you like!) Indeed, we can make Exc an instance of the above by
> instance MonadExc Exc where
> throw = ExnI urge you to directly enter the body of evalExc above into GHCi and see what type is inferred for it!
Similarly, we can bottle the notion of a state(-transforming) monad in the typeclass
> class Monad m => MonadST m where
> runStateST :: m a -> StateST -> m (a, StateST)
> getST :: m StateST
> putST :: StateST -> m ()which corresponds to monads that are kitted out with the appropriate execution, extraction and modification functions. Needless to say, we can make ST an instance of the above by
> instance MonadST ST where
> runStateST (S f) = return . f
> getST = S (\s -> (s, s))
> putST = \s' -> S (\_ -> ((), s'))Once again, if you know whats good for you, enter the body of evalST into GHCi and see what type is inferred.
Armed with these two typeclasses, we can write our evaluator quite easily
> tickST = do
> n <- getST
> putST (n + 1)> evalMega (Val n) = return n
> evalMega (Div x y) = do n <- evalMega x
> m <- evalMega y
> tickST
> if m == 0
> then throw $ errorS y m
> else return $ n `div` mWhat is the type of evalMega ?
Expr -> ST IntExpr -> Exc Int(MonadST m) => Expr -> m Int(MonadExc m) => Expr -> m Int(MonadST m, MonadExc m) => Expr -> m Int
Note that it is simply the combination of the two evaluators from before – we use the throw from evalExc and the tickST from evalST. Meditate for a moment on the type of above evaluator; note that it works with any monad that is both a exception- and a state- monad!
Indeed, if, as I exhorted you to, you had gone back and studied the types of evalST and evalExc you would find that each of those functions required the underlying monad to be a state-manipulating and exception-handling monad respectively. In contrast, the above evaluator simply demands both features.
Next: But … how do we create monads with both features**?
SKIP to step 5
To add special features to existing monads, we will use monad transformers, which are type operators t that map a monad m to a monad t m. The key ingredient of a transformer is that it must have a function promote that can take an m value (ie action) and turn it into a t m value (ie action):
> class Transformer t where
> promote :: Monad m => m a -> (t m) aNow, that just defines the type of a transformer, lets see some real transformers!
A Transformer For Exceptions
Consider the following type
> newtype ExcT m a = MkExc (m (Exc a))it is simply a type with two parameters – the first is a monad m inside which we will put the exception monad Exc a. In other words, the ExcT m a simply injects the Exc a monad into the value slot of the m monad.
It is easy to formally state that the above is a bonafide transformer
> instance Transformer ExcT where
> promote = MkExc . promote_where the generic promote_ function simply injects the value from the outer monad m into the inner monad m1 :
> promote_ :: (Monad m, Monad m1) => m t -> m (m1 t)
> promote_ m = do x <- m
> return $ return xConsequently, any operation on the input monad m can be directly promoted into an action on the transformed monad, and so the transformation preserves all the operations on the original monad.
Now, the real trick is twofold, we ensure that if m is a monad, then transformed ExcT m is an exception monad, that is an MonadExc.
First, we show the transformer output is a monad:
> instance Functor m => Functor (ExcT m) where
> instance Applicative m => Applicative (ExcT m) where> instance Monad m => Monad (ExcT m) where
> return x = promote $ return x
> p >>= f = MkExc $ strip p >>= r
> where r (Result x) = strip $ f x
> r (Exn s) = return $ Exn s
> strip (MkExc m) = mand next we ensure that the transformer is an exception monad by equipping it with throw
> instance Monad m => MonadExc (ExcT m) where
> throw s = MkExc $ return $ Exn sA Transformer For State
Next, we will build a transformer for the state monad, following, more or less, the recipe for exceptions. Here is the type for the transformer
> newtype STT m a = MkSTT (StateST -> m (a, StateST))Thus, in effect, the enhanced monad is a state-update where the output is the original monad as we do the state-update and return as output the new state wrapped inside the parameter monad.
> instance Transformer STT where
> promote f = MkSTT $ \s -> do x <- f
> return (x, s)Next, we ensure that the transformer output is a monad:
> instance Functor m => Functor (STT m) where
> instance Applicative m => Applicative (STT m) where
> instance Monad m => Monad (STT m) where
> return = promote . return
> m >>= f = MkSTT $ \s -> do (x, s') <- strip m s
> strip (f x) s'
> where strip (MkSTT f) = fand next we ensure that the transformer is a state monad by equipping it with the operations from MonadST
> instance Monad m => MonadST (STT m) where
> --runStateST :: STT m a -> StateST -> STT m (a, StateST)
> runStateST (MkSTT f) s = MkSTT $ \s0 -> do (x,s') <- f s
> return ((x,s'), s0)
> --getST :: STT m StateST
> --getST :: MkSTT (StateST -> m (StateST, StateST))
> getST = MkSTT $ \s -> return (s, s)
>
> --putST :: StateST -> STT m ()
> --putST :: StateST -> MkSTT (StateST -> m ((), StateST))
> putST s = MkSTT (\_ -> return ((), s))Of course, we must make sure that the original features of the monads are not lost in the transformed monads. For this purpose, we will just use the promote operation to directly transfer operations from the old monad into the transformed monad.
Thus, we can ensure that if a monad was already a state-manipulating monad, then the result of the exception-transformer is also a state-manipulating monad.
> instance MonadExc m => MonadExc (STT m) where
> throw s = promote (throw s)> instance MonadST m => MonadST (ExcT m) where
> getST = promote getST
> putST = promote . putST
> runStateST (MkExc m) s = MkExc $ do (ex, s') <- runStateST m s
> case ex of
> Result x -> return $ Result (x, s')
> Exn err -> return $ Exn errRecap: Exception Transformer
-- An exn transformer
newtype ExcT m a = MkExc (m (Exc a))
-- Transformation IS a monad
instance Monad m => Monad (ExcT m) where
...
-- Transformation ADDs Exn-ness
instance Monad m => MonadExc (ExcT m) where
...
-- Transformation PRESERVES ST-ness
instance MonadST m => MonadST (ExcT m) whereRecap: State Transformer
newtype STT m a = MkSTT (StateST -> m (a, StateST))
...
-- Transformation IS a monad
instance Monad m => Monad (STT m) where
...
-- Transformation PRESERVES Exn-ness
instance MonadExc m => MonadExc (STT m) where
...
-- Transformation ADDs ST-ness
instance Monad m => MonadST (STT m) whereFinally, we can put all the pieces together and run the transformers. We could order the transformations differently (and that can have different consequences on the output as we will see.)
> type StEx a = STT Exc a
> type ExSt a = ExcT ST a> evalExSt :: Expr -> ExSt Int
> evalExSt = evalMega
>
> evalStEx :: Expr -> StEx Int
> evalStEx = evalMegawe can extract the values from the monadic action by running the actions from a given start state (here the initial counter 0)
> runStEx :: StEx a -> Exc (a, Int)
> runStEx (MkSTT f) = f 0
>
> runExSt :: ExSt a -> (Exc a, Int)
> runExSt (MkExc (S f)) = f 0which, given the rendering functions:
> instance Show a => Show (StEx a) where
> show m = case runStEx m of
> Exn s -> "Exn:" ++ s ++ "\n"
> Result (v, cnt) -> "Count:" ++ show cnt ++ "\n" ++
> "Result: " ++ show v ++ "\n"
>
> instance Show a => Show (ExSt a) where
> show m = "Count: " ++ show cnt ++ "\n" ++ show r ++ "\n"
> where
> (r, cnt) = runExSt mwe can now evaluate the expressions in GHCi:
ghci> evalStEx err
Exn:Error dividing by Div (Val 2) (Val 3) = 0
ghci> evalStEx ok
Count: 2
Result 42
ghci> evalExSt err
Count: 2
Exn "Error dividing by Div (Val 2) (Val 3) = 0"
ghci> evalExSt ok
Count:2
Result: 42While it is often instructive to roll your own versions of code, as we did above, in practice you should reuse as much as you can from standard libraries.
The above sauced-up exception-tracking version of Maybe already exists in the standard type Either
ghci> :info Either
data Either a b = Left a | Right b -- Defined in Data.EitherThe Either type is a generalization of our Exc type, where the exception is polymorphic, rather than just being a String. In other words the hand-rolled Exc a corresponds to the standard Either String a type.
The standard MonadError typeclass corresponds directly with MonadExc developed above.
ghci> :info MonadError
class (Monad m) => MonadError e m | m -> e where
throwError :: e -> m a
catchError :: m a -> (e -> m a) -> m a
-- Defined in Control.Monad.Error.Class
instance (Monad m, Error e) => MonadError e (ErrorT e m)
-- Defined in Control.Monad.Error
instance (Error e) => MonadError e (Either e)
-- Defined in Control.Monad.Error
instance MonadError IOError IO -- Defined in Control.Monad.ErrorNote that Either String is an instance of MonadError much like Exc is an instance of MonadExc. Finally, the ErrorT transformer corresponds to the ExcT transformer developed above and its output is guaranteed to be an instance of MonadError.
Similarly, the ST monad that we wrote above is but a pale reflection of the more general State monad.
ghci> :info State
newtype State s a = State {runState :: s -> (a, s)}
-- Defined in Control.Monad.State.LazyThe MonadST typeclass that we developed above corresponds directly with the standard MonadState typeclass.
ghci> :info MonadState
class (Monad m) => MonadState s m | m -> s where
get :: m s
put :: s -> m ()
-- Defined in Control.Monad.State.Class
instance (Monad m) => MonadState s (StateT s m)
-- Defined in Control.Monad.State.Lazy
instance MonadState s (State s)
-- Defined in Control.Monad.State.LazyNote that State s is already an instance of MonadState much like ST is an instance of MonadST. Finally, the StateT transformer corresponds to the STT transformer developed above and its output is guaranteed to be an instance of MonadState.
Thus, if we stick with the standard libraries, we can simply write
> tick :: (MonadState Int m) => m ()
> tick = do {n <- get; put (n+1)}
>
> eval1 :: (MonadError String m, MonadState Int m) => Expr -> m Int
> eval1 (Val n) = return n
> eval1 (Div x y) = do n <- eval1 x
> m <- eval1 y
> if m == 0
> then throwError $ errorS y m
> else do tick
> return $ n `div` mwe can create a concrete instance by defining:
> type SE a = StateT Int (Either String) a> evalSE :: Expr -> SE Int
> evalSE = eval1
>
> runSE :: SE a -> Either String (a, Int)
> runSE m = runStateT m 0Which lets us evaluate an expression as:
ghci> runSE (evalSE ok)
Right (42,2)
ghci> runSE (evalSE err)
Left "Error dividing by Div (Val 2) (Val 3) = 0"You can stack them in the other order if you prefer
> type ES a = ErrorT String (State Int) a
>
> evalES :: Expr -> ES Int
> evalES = eval1
>
> runES :: ES a -> (Either String a, Int)
> runES m = runState (runErrorT m) 0which will yield a different result
ghci> runES (evalES ok)
(Right 42,2)
ghci> runES (evalES err)
(Left "Error dividing by Div (Val 2) (Val 3) = 0",2)see that we actually get the division-count (upto the point of failure) even when the computation bails.
Note: the different types of evalES, evalSE and runES, runSE. These arise from the different order in which the monads are stacked.
Next, we will spice up our computations to also log messages (a pure variant of the usual method where we just print the messages to the screen.) This can be done with the standard Writer monad, which supports a tell action that logs the string you want (and allows you to later view the entire log of the computation.
To accomodate logging, we juice up our evaluator directly as
> eval2 v =
> case v of
> Val n -> do tell $ msg v n
> return n
> Div x y -> do n <- eval2 x
> m <- eval2 y
> if m == 0
> then throwError $ errorS y m
> else do tick
> tell $ msg v (n `div` m)
> return $ n `div` mwhere the msg function is simply
> msg t r = "term: " ++ show t ++ ", yields " ++ show r ++ "\n"Note that the only addition to the previous evaluator is the tell operations! We can run the above using
> evalWSE :: Expr -> WSE Int
> evalWSE = eval2where WSE is a type abbreviation
> type WSE a = WriterT String (StateT Int (Either String)) aThat is, we simply use the WriterT transformer to decorate the underlying monad that carries the state and exception information.
We can then create a function that executes an WSE a action:
> runWSE m = runStateT (runWriterT m) 0ghci> runWSE (evalWSE ok)
Right ((42,"term: Val 1972, yields 1972\nterm: Val 2, yields 2\nterm: Div (Val 1972) (Val 2), yields 986\nterm: Val 23, yields 23\nterm: Div (Div (Val 1972) (Val 2)) (Val 23), yields 42\n"),2)
ghci> runWSE (evalWSE err)
Left "Error dividing by Div (Val 2) (Val 3) = 0"That looks a bit ugly, so we can write our own pretty-printer
> instance Show a => Show (WSE a) where
> show m = case runWSE m of
> Left s -> "Error: " ++ s
> Right ((v, w), s) -> "Log:\n" ++ w ++ "\n" ++
> "Count: " ++ show s ++ "\n" ++
> "Value: " ++ show v ++ "\n"after which we get
ghci> evalWSE ok
Log:
term: Val 1972, yields 1972
term: Val 2, yields 2
term: Div (Val 1972) (Val 2), yields 986
term: Val 23, yields 23
term: Div (Div (Val 1972) (Val 2)) (Val 23), yields 42
Count: 2
Value: 42
ghci> print $ evalWSE err
Error: Error dividing by Div (Val 2) (Val 3) = 0How come we didn’t get any log in the error case?
The answer lies in the order in which we compose the transformers; since the error wraps the log, if the computation fails, the log gets thrown away. Instead, we can just wrap the other way around
> type ESW a = ErrorT String (StateT Int (Writer String)) a
>
> evalESW :: Expr -> ESW Int
> evalESW = eval2
>
> runESW :: ESW a -> ((Either String a, Int), String)
> runESW m = runWriter (runStateT (runErrorT m) 0)
>
> instance Show a => Show (ESW a) where
> show m = "Log:\n" ++ log ++ "\n" ++
> "Count: " ++ show cnt ++ "\n" ++
> result
> where
> ((res, cnt), log) = runESW m
> result = case res of
> Left s -> "Error: " ++ s
> Right v -> "Value: " ++ show vafter which, everything works just fine!
ghci> evalESW err
Log:
term: Val 2, yields 2
term: Val 1, yields 1
term: Val 2, yields 2
term: Val 3, yields 3
term: Div (Val 2) (Val 3), yields 0
Count: 1
Error: Error dividing by Div (Val 2) (Val 3) = 0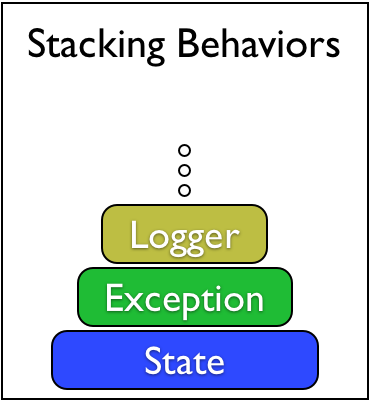
There are many useful monads, and if you play your cards right, Haskell will let you stack them nicely on top of each other, so that you can get mega-monads that have all the powers of the individual monads. See for yourself in Homework 3.